[ Einführung ] - [ Einleitung ] - [ Dynamische Systeme ] - [ Wachstumsfunktionen ] - [ Räuber-Beute-Modell ] - [ Bevölkerungsmodelle ] - [ Modelle in der Physik ] - [ Literaturverzeichnis ]
2. Dynamische Systeme und ihre Beschreibung
Ein System besteht aus mehreren Komponenten meist recht verschiedener Art, die durch Wirkungsbeziehungen miteinander verknüpft sind. Alle Systeme, die ein zeitabhängiges Verhalten zeigen, d.h. deren Entwicklung nur von der Zeit als unabhängigen Variablen abhängt, bezeichnen wir als dynamische Systeme. Das Systemverhalten ergibt sich dabei aus dem Zusammenspiel der Komponenten. Diese Komponenten lassen sich für alle dynamischen Systeme folgendermaßen unterteilen:
- Parameter oder Konstanten sind Größen, die über die Beobachtungszeit konstant bleiben. Oft sind es Naturkonstanten, wie z.B. die Sonneneinstrahlung.
- Exogene Größen sind Veränderliche, die auf das System einen Einfluß haben, auf die das System selbst aber keinen Einfluß nehmen kann.
- Zustandsgrößen werden oft auch als Bestands- oder Speichergrößen bezeichnet. Ihr jeweiliger Zustand kennzeichnet auch gleichzeitig den Zustand des Gesamtsystems. Sie sind deshalb für die Entwicklung des Systems und für seine Beschreibung und Simulation von zentraler Bedeutung.
- Anfangswerte der Zustandsgrößen bestimmen demnach die weitere Entwicklung eines Systems entscheidend und müssen deshalb auch bekannt sein.
- Die Flüsse oder Veränderungsraten der Zustandsgrößen bestimmen, ob und wie die Zustandsgrößen zunehmen und abnehmen. Sie müssen daher bekannt sein, um die weitere Entwicklung des Systems zu ermitteln.
- Zwischengrößen oder Funktionen sind Größen, die sich zwar im Laufe der Zeit verändern, die aber ständig aus dem Systemzustand, also aus den Zustandsgrößen, berechenbar sind.
Die Einsicht, daß gänzlich verschiedene Systeme die grundsätzlich gleichen Kategorien von Systemelementen haben, vereinfacht die weiteren Untersuchungen konkreter Systeme enorm. Wir können jetzt nämlich die gleichen Bezeichnungen, die gleichen Symbole, die gleiche mathematische Beschreibung und gleiche Computerprogramme verwenden, um die Entwicklung völlig verschiedener dynamischer Systeme zu untersuchen.
Wirkungsdiagramme und Simulationsdiagramme. Wir verwenden hier zwei Arten von Diagrammen, um Modelle darzustellen. Das Wirkungsdiagramm (Kausaldiagramm) ist eine erste, noch nicht quantifizierte Darstellung der Wirkungsbeziehung im System. Die Pfeile zeigen, wie Systemgrößen auf andere einwirken. Ein Pfeil von A nach B bedeutet: „A wirkt auf B“.
Wir verwenden hier die Symbolsprache der System Dynamics (z.B. Stella, Meadows: Grenzen des Wachtums). Diese Symbolik stellt durch 'Ventile' und 'Behälter' die 'Flüsse' (Veränderungsraten) und 'Speicherinhalte' (Zustände) plastisch dar und macht damit des Funktionieren des Systems sehr einsichtig. Im Simulationsdiagramm werden ebenfalls die Wirkungen zwischen den Größen gezeigt. Die Struktur ist die gleiche wie im Wirkungsdiagramm. Doch jetzt werden auch die verschiedenen Arten der Größen unterschieden. Es wird die Art der Verknüpfungen zwischen den Systemgrößen definiert.
 | Parameter, exogene Größe |
 | Tabellenfunktion |
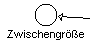 | Zwischengröße |
 | Zustandsgröße, Bestandsgröße |
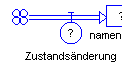 | Zustandsänderung, Veränderungsrate, Fluss |
Als Symbole zur Erstellung von Simulationsdiagrammen werden, Kreise und Rechtecke verwendet. Parameter oder exogene Funktionen der Zeit werden mit roten Kreisen gekennzeichnet, sie haben keine Eingänge (Eingangspfeile). Eine exogene Tabellenfunktion wird durch eine Tilde (~) markiert.
Zwischengrößen werden durch einen Kreis gekennzeichnet, Zustandsgrößen (Bestandsgrößen, Speichergrößen) erscheinen als Rechteck.
Für jeden Block lässt sich also eine Rechenanweisung angeben. Für die Zustandsgrößen (Integrator) wird eine spezielle Rechenvorschrift verwendet, die den neuen Wert aus dem alten Wert zuzüglich der Veränderung während des Zeitschritts berechnet. Zu Anfang der Rechnung entspricht der alte Wert dem vorgegebenen Anfangswert. Diese Gleichungen werden von DYNASYS automatisch erzeugt.