<html>
</html> [ Einführung ] - [ Einleitung ] - [ Dynamische Systeme ] - [ Wachstumsfunktionen ] - [ Räuber-Beute-Modell ] - [ Bevölkerungsmodelle ] - [ Modelle in der Physik ] - [ Literaturverzeichnis ] <html>
</html>
5. Bevölkerungsmodell mit drei Altersklassen
Die im letzten Kapitel betrachteten Wachstumsfunktionen beschreiben die Bevölkerungsentwicklung oft nur unzureichend. Sie sind höchstens für die Simulation des Wachstums von Bakterienkulturen geeignet. Fehler entstehen vor allem dadurch, daß man von einer homogenen Bevölkerung ausgeht, deren Altersstruktur völlig unberücksichtigt bleibt. Es macht offensichtlich einen Unterschied, ob eine Bevölkerung vorwiegend aus Kindern und Erwachsenen im reproduktionsfähigen Alter oder aus Alten besteht. Alte tragen zur Reproduktion nicht bei, Kinder noch nicht. Zur Berechnung der Geburtenzahlen muß daher die Zahl der gebährfähigen Mütter und deren Fertilität (Fruchtbarkeit) bekannt sein. Erst in einem Modell, das die wichtigsten Altersgruppen enthält, können zuverlässige Angaben über den Bedarf an infrastrukturellen Maßnahmen (Bau von Kindergärten, Schulen etc.) bzw. über Staatsausgaben und wirtschaftliche Entwicklung gemacht werden.
Wir benutzen hier ein Modell mit nur drei Altersklassen, das aber schon erstaunlich gute Vorhersagen zulässt:
- Kinder im Alter von 0 bis 16 Jahren.
- Eltern im Alter von 17 - 45 Jahren, wobei es genauso viele Frauen wie Männer gibt.
- Alte älter als 45 Jahre.
Die Gesamtbevölkerung ergibt sich aus der Summe der drei Bevölkerungsgruppen. Jede Bevölkerungsgruppe hat eine altersspezifische Sterberate, die bei der Gruppe der Alten am höchsten ist. Die Gruppe der Kinder hat Zuwachs durch die Neugeborenen, jeweils 1/16 der Gruppe der Kinder geht pro Jahr über in die Gruppe der Erwachsenen. Ein ähnlicher Übergang findet zwischen der Gruppe der Eltern und der Alten statt.
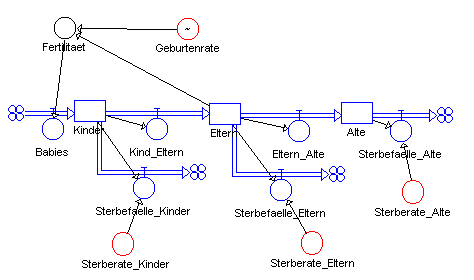
Die Geburtenrate beträgt in der Bundesrepublik z.Z. 1,2 Kind pro Frau. Die Zahl der Kinder muss noch auf 29 Jahre verteilt werden, so daß man die Fertilität (Zahl der Neugeborenen pro Jahr und Frau) durch Division der Geburtenrate durch 29 erhält. Damit ergibt sich das folgende Simulationsdiagramm:
Simulationsdiagramm für das Wachstumsmodell
</html>
Die Angaben im folgenden Simulationsgleichungen sind in Millionen. Die Tabellenfunktion ist an dieser Stelle zwar überflüssig, mit ihr kann man aber leicht eine Veränderung der Geburtenrate realisieren.
Zustandsgleichungen
Kinder.neu <-- Kinder.alt + dt*(Babies-Kind_Eltern-Sterbefaelle_Kinder)
Startwert Kinder = 13
Eltern.neu <-- Eltern.alt + dt*(Kind_Eltern-Eltern_Alte-Sterbefaelle_Eltern)
Startwert Eltern = 23
Alte.neu <-- Alte.alt + dt*(Eltern_Alte-Sterbefaelle_Alte)
Startwert Alte = 21
Konstanten
Geburtenrate = 1.2
Sterberate_Alte = 0.025
Sterberate_Eltern = 0.005
Sterberate_Kinder = 0.004
Zustandsänderungen
Babies = Fertilitaet
Kind_Eltern = Kinder*(1/16)
Eltern_Alte = Eltern*(1/29)
Sterbefaelle_Alte = Alte*Sterberate_Alte
Sterbefaelle_Eltern = Eltern*Sterberate_Eltern
Sterbefaelle_Kinder = Sterberate_Kinder*Kinder
Zwischenwerte
Fertilitaet = Eltern*Geburtenrate*0.5/29
Das Diagramm in Abb. 3.17 zeigt das Simulationsergebnis bei konstanter Geburtenrate. Man erkennt die Änderung der Altersstruktur. Es gibt immer mehr ältere Menschen, während die Zahl der Kinder und Eltern abnimmt. Etwa im Jahr 2010 hat die Zahl der alten Menschen ein Maximum.
Bevölkerungsentwicklung bei einer konstanten Fertlität von 1,2
</html>
Entwicklungsländer haben eine völlig andere Altersstruktur als entwickelte Länder. Die Angaben in der Tabelle für das Land Kenia entstammen wie alle anderen Daten zum Modell der Bevölkerung mit drei Klassen BOS85. In Global 2000 GLO80 ist ein Kapitel der Bevölkerungsprognostik gewidmet. Dort wird ausführlich das Kohortenmodell besprochen, das aus jedem Jahrgang eine Altersgruppe bildet und somit ein genaueres Modell darstellt. Gleichzeitig wird aber auch auf die Schwierigkeiten bei der Prognose der Bevölkerungsentwicklung hingewiesen, die vor allem im Bereich der Datenerhebung liegen. Vor allen bei Ländern der dritten Welt kann oft nur mit Annahmen und Schätzungen gearbeitet werden.
Altersverteilung und Sterblichkeit in Kenia: <html>
</html>
| Altersgruppe | Bevölkerung in Mio. | Sterblichkeit |
|---|---|---|
| Kinder | 7,5 | 0,004 |
| Eltern | 6,0 | 0,005 |
| Alte | 1,5 | 0,05 |
<html>
</html>
Aufgabe
Untersuchen Sie die Bevölkerungsentwicklung Kenias, wenn es bei der bisherigen Zahl von 7,5 Kindern pro Frau bleibt. Verändern Sie danach das Modell so, daß sich bis zum Jahr 2000 die Geburtenrate auf 2,1 reduzieren läßt. An den Ergebnissen wird deutlich, wie groß der Einfluß der Anzahl der Geburten auf die Bevölkerungsentwicklung ist und an welcher Stelle somit politische Maßnahmen getroffen werden müssen. Auf alle Fälle wird es einen starken Anstieg alter Menschen geben.