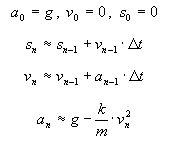6. Dynamische Systeme in der Physik

Viele physikalische Vorgänge lassen sich mit dynamischen Systemen beschreiben. Dadurch können auch mathematisch anspruchsvolle Zusammenhänge mit einfachen Mitteln quantitativ erfaßt werden. Dies wird im Folgenden an zwei Beispielen verdeutlicht.

6.1 Abkühlungsvorgang

Lässt man eine Tasse heißen Kaffee eine Zeit lang stehen, kühlt sich der Kaffee bis auf die Umgebungstemperatur ab. Die Abkühlung erfolgt um so schneller, je größer die Temperaturdifferenz zwischen der Temperatur des Kaffees und der Umgebung ist. Außerdem gehen noch die Wärmeleitfähigkeit der Tasse und das Verhältnis von Volumen und Oberfläche als Abkühlungsfaktor in das System als Konstante ein.

Somit lässt sich der ganze Abkühlungsvorgang durch das Simulationsdiagramm in folgender Abbildung beschreiben.

<html>

Simulationsdiagramm des Abkühlungsvorgangs

</html>

Das entsprechende Simulations-Programm:

 Zustandsgleichungen 
     Temperatur.neu <-- Temperatur.alt + dt*(-Abkuehlung)
     Startwert Temperatur = 95
 
 Konstanten 
      Abkuehlungsfaktor = 0.5
      Aussentemperatur = 18
  
 Raten 
      Abkuehlung = Tempdifferenz*Abkuehlungsfaktor
  
 Zwischenwerte 
      Tempdifferenz = Temperatur-Aussentemperatur

6.2 Mutter-Tochter-Radioaktivität

Es gibt eine Vielzahl von Stoffen, die nicht stabil sind. Unter Aussendung von Alpha- bzw. Betastrahlen (positiv geladenen Heliumkernen bzw. Elektronen) wandeln sich die Atomkerne um. Diese Zerfallsprozesse erfolgen völlig ungeordnet. Betrachtet man aber eine größere Anzahl von Atomkernen, so folgt dieser Zerfall mit großer Genauigkeit dem radioaktiven Zerfallsgesetz. Dabei besitzt jede Atomsorte eine charakteristische Zerfallskonstante. Hierdurch sind zum Beispiel Altersbestimmungen nach der C-14-Methode in der Archäologie mit großer Genauigkeit möglich.

Betrachtet man eine bestimmte Atomart (z.B. Uran), so erhält man Zerfallsreihen: Der Urankern zerfällt und wandelt sich mit seiner spezifischen Zerfallskonstanten in Radon um usw. Am Ende dieser Kette steht ein stabiles Element.

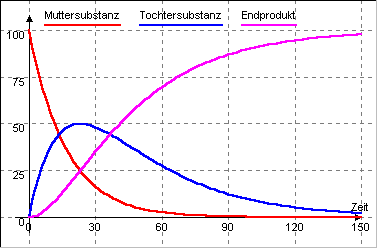
Betrachtet man zunächst ein Element für sich, so liegt hier ein exponentieller Zerfall vor. Je mehr Atome noch vorhanden sind, desto mehr Atome zerfallen. Das Zerfallsprodukt (Tochtersubstanz) kann jetzt selbst wieder radioaktiv sein und mit einer zweiten Zerfallsrate zerfallen. Das hierbei entstehende Endprodukt bleibt dann stabil.

Dieser Vorgang läßt sich sehr gut am Flussdiagramm nachvollziehen.

<html>

Abb.: Mutter-Tochter-Radioaktivität

</html>

Das entsprechende Simulationsprogramm lautet:

 Zustandsgleichungen 
     Muttersubstanz.neu <-- Muttersubstanz.alt + dt*(-Mutteraktivitaet)
       Startwert Muttersubstanz = 100
     Tochtersubstanz.neu <-- Tochtersubstanz.alt + dt*(Mutteraktivitaet-Tochteraktivitaet)
       Startwert Tochtersubstanz = 0
     Endprodukt.neu <-- Endprodukt.alt + dt*(Tochteraktivitaet)
       Startwert Endprodukt = 0
  
 Zustandsänderungen 
      Mutteraktivitaet = Zerfallsrate_Mutter*Muttersubstanz
      Tochteraktivitaet = Zerfallsrate_Tochter*Tochtersubstanz
 
 Konstanten 
      Zerfallsrate_Mutter = 0.06
      Zerfallsrate_Tochter = 0.03

<html>

Ergebnis der Simulation des radioaktiven Zerfalls

</html>

6.3 Modell für einen Fallschirmspringer

Ein Fallschirmspringer mit Masse m springt in Höhe h mit der Anfangsgeschwindigkeit 0 m/s aus dem Flugzeug. Der Luftwiderstand W sei proportional zum Quadrat der Geschwindigkeit (W=kv). Der Reibungskoeffizient k beträgt bei geschlossenem Fallschirm ungefähr 0,3 kg/m, bei geöffnetem Fallschirm 30 kg/m.

Von Interesse sind Höhe, Geschwindigkeit und Beschleunigung des Fallschirmspringers, speziell die Grenzgeschwindigkeit beim freien Fall mit ungeöffnetem Fallschirm und die Geschwindigkeit bei der Landung. Aber auch die auftretenden Kräfte beim Öffnen des Fallschirms oder der Einfluss verschiedener Parameter wie die Größe des Fallschirms, Gewicht des Fallschirmspringers usw. liefern interessante Fragestellungen.

Mit dem folgenden Modell kann der Flug des Fallschirmspringers recht genau simuliert werden. Ausgehend vom 2. Newtonschen Gesetz können die Weg-, Geschwindigkeits- und Beschleunigungsfunktion näherungsweise berechnet werden.

Mit der Diskretisierung 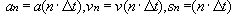erhält man für genügend kleine Werte von 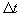die Rekursionsformeln

liefert die Höhe des Fallschirmspringers im Zeitpunkte n * 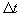. Diese Gleichungen lassen sich leicht in das nebenstehende DYNASYS-Modell umformen.

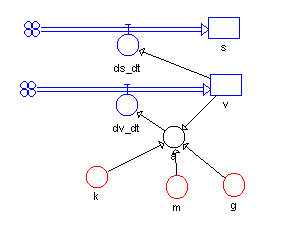
k, m und g sind die Parameter des Modells. k wird in den folgenden Simulationsläufen in den ersten 15 s mit k=0,03 kg/m angenommen, danach wird der Fallschirm gezogen und Wert ändert sich auf k=30 kg/m, m=80 kg und g=9,81 m/s.

<html>

Abb.: Flussdiagramm Fallschirmspringer

</html>

 Zustandsgleichungen 
     v.neu <-- v.alt + dt*(dv_dt)
       Startwert v = 0
     s.neu <-- s.alt + dt*(ds_dt)
       Startwert s = 0
  
 Zustandsänderungen 
      dv_dt = a
      ds_dt = v
 
 Konstanten 
      m = 80
      g = 9.81
      k = Wenn(Zeit>15;30;0.3)
  
 Zwischenwerte 
      a = g-(k/m*v*v)

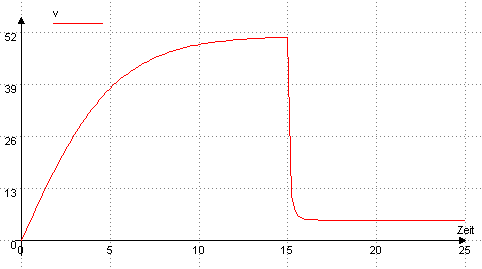
Für die ersten 25 s ergibt sich das folgende Diagramme:

<html>

Abb.: Geschwindigkeit des Fallschirmspringers

</html>