4. Das Räuber-Beute-Modell

In den über mehr als neun Jahrzehnte geführten Aufzeichnungen der Hudson-Bay-Company über den Eingang von Fellen von Luchsen und Schneehasen finden sich starke und regelmäßige Schwankungen mit einer Periode von 6,9 Jahren. Auf ähnliche periodische Schwankungen von Fischbeständen in der Adria hingewiesen, formulierte Vito Volterra 1931 ein mathematisches Modell, das die Dynamik von Räuber-Beute-Systemen beschreibt. Unabhängig von ihm entwickelte Alfred Lotka den gleichen Ansatz. Ihre Arbeit ist unter dem Begriff Lotka-Volterra-System bekannt geworden.

<html>

Aufzeichnungen der Hudson-Bay-Company über den Eingang von Fellen von Luchsen und Schneehasen

</html>

Wir werden hier das Modell eines Räuber-Beute-Systems bei begrenzter Weidehaltung entwickeln. Zunächst werden die beiden Populationen von Füchsen und Hasen getrennt betrachtet. Betrachtet man allein die Fuchspopulation, so ergibt sich das Simulationsdiagramm aus Abb. 3.10.

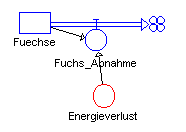
<html>

Modellteil für den Fuchsbestand im Räuber-Beute-System

</html>

Der Fuchsbestand vergrößert sich mit der Zufuhr von Futter, und er verringert sich entsprechend dem Energieverlust zur Erhaltung der Lebensvorgänge. Dieser Erhaltungsbedarf ist hier mit 0,2/Woche angesetzt, d.h. ohne Nahrungszufuhr würde ein Fuchs 20% seines Gewichts (genauer seines Energieinhalts) pro Woche verlieren. Im Gleichgewichtszustand müßte die Nahrungszufuhr genau dieser Menge entsprechen.

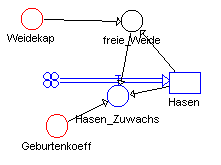
<html>

Modellteil für den Hasenbestand im Räuber-Beute-System

</html>

Das Simulationsdiagramm für die Hasen zeigt Abb. 3.11. Wir nehmen zunächst einmal an, daß die Hasenpopulation bei ungehindertem Wachstum eine Nettozuwachsrate von 0,08 pro Woche haben würde, was einer Verdopplung in etwa 9 Wochen entspricht.

Bei begrenzter Weidekapazität wird dieser Zuwachs jedoch auf Null reduziert, wenn die Weidekapazität (z.B. 1000 Hasen) voll ausgenutzt wird. Der Hasenbestand verringert sich durch Verluste an die Füchse. Die Kopplung zwischen den beiden Populationen läßt sich durch das Simulationsdiagramm in Abb. 3.12 beschreiben.

Je mehr Hasen es gibt, um so mehr stehen den Füchsen als Beute zur Verfügung. Je mehr Füchse es gibt, um so mehr Hasen werden den Füchsen zur Beute fallen. Das Produkt aus Hasen und Füchsen kann daher als Maß dafür genommen werden, wie viele Hasen den Füchsen zur Beute fallen. Jeder erlegte Hase bringt dem Fuchsbestand einen entsprechenden Gewinn und bedeutet einen entsprechenden Verlust für den Hasenbestand. Für die Festlegung der Faktoren gelten folgende Überlegungen: bei einer mittleren Zahl von 500 Hasen und 10 Füchsen (Treffen=5000/Woche) sollen die Füchse ihre Verluste von 10*0,2=2 ersetzen können. Hieraus ergibt sich die Gewichtung der Verbindung von Treffen zu Füchsen als 2/5000=0,0004. Wird angenommen, daß ein Fuchs die Biomasse von 5 Hasen hat, so entspricht dieser Gewinn von 2 Fuchseinheiten pro Woche einem Verlust von 10 Hasen pro Woche. Der Wichtungsfaktor für die Verbindung Treffen nach Hasen wird also -10/5000=-0,002.

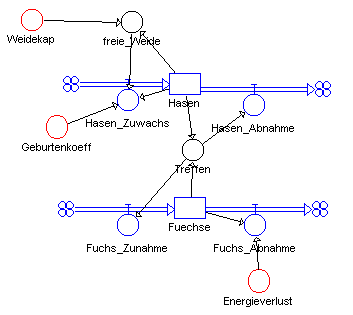
<html>

Verkopplung beider Modellteile

</html>

Aus diesen Bausteinen können wir nun das Gesamtmodell zusammensetzen.

 Zustandsgleichungen
    Hasen.neu <-- Hasen.alt + dt*(Hasen_Zuwachs-Hasen_Abnahme) 
    Startwert Hasen = 200
    Fuechse.neu <-- Fuechse.alt + dt*(Fuchs_Zunahme-Fuchs_Abnahme) 
    Startwert Fuechse = 50
     
 Konstanten
    Energieverlust = 0.2 
    Geburtenkoeff = 0.08
     
 Raten
    Hasen_Zuwachs = 0.001*Hasen*freie_Weide*Geburtenkoeff 
    Hasen_Abnahme = 0.002*Treffen
    Fuchs_Zunahme = 0.0004*Treffen 
    Fuchs_Abnahme = Energieverlust*Fuechse
     
 Zwischenwerte
    freie_Weide = Weidekap-Hasen 
    Treffen = Hasen*Fuechse
    Weidekap = Wenn (Zeit<=100;2000;1000)

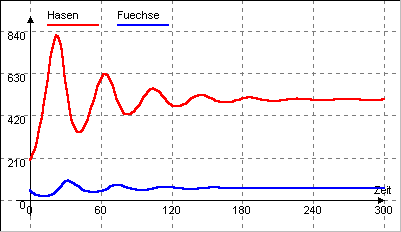
<html>

Ergebnis der Simulation des Räuber-Beute-Systems

</html>

Statt eines konstanten Wertes kann man eine Halbierung der Weidekapazität nach einer bestimmten Zeit durchführen. Dies erreicht man einfachsten durch eine Tabellenfunktion.